Accueil > 02 - Livre Deux : SCIENCES > Atome : lois de la Physique ou rétroaction de la matière/lumière et du (...) > Résonance et rythmologie de la matière/lumière
Résonance et rythmologie de la matière/lumière
samedi 25 novembre 2017, par

Voilà un exemple de résonance : celle entre le rythme du vent et la période propre du pont : la résonance va amplifier les vibrations au point de casser le pont !!!




Voilà un autre exemple de résonance : celle des pendules couplés

Et (ci-dessous) deux métronomes dont les vibrations sont couplées par résonance :





Voici un tout autre exemple : les cellules cardiaques qui sont des oscillateurs couplés


Phénomène de résonance quantique

Résonance de l’archet et du violoncelle

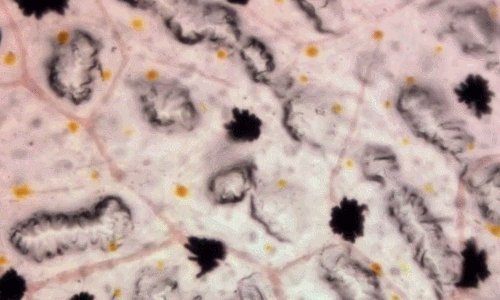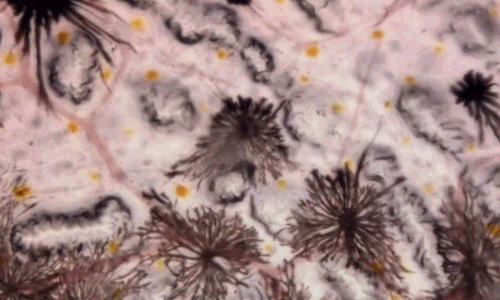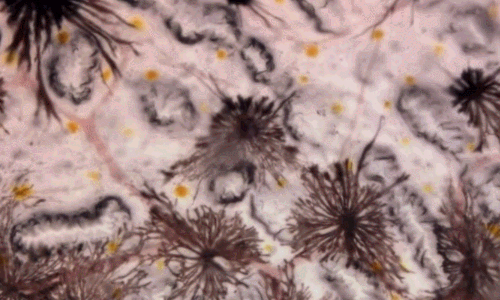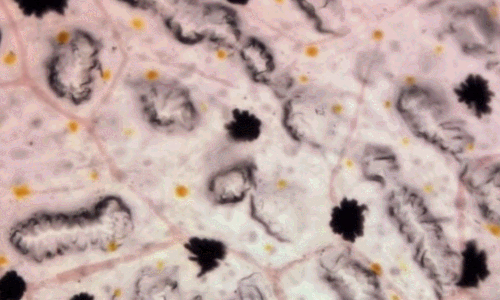
Poudres sur une plaque vibrante

Voilà la résonance entre la fréquence propre d’un verre et celle de la vibration qui le casse :

Résonance et rythmologie de la matière/lumière
Diderot dans « Entretien entre d’Alembert et Diderot :
« C’est ce qui m’a fait quelquefois comparer les fibres de nos organes à des cordes vibrantes sensibles. La corde vibrante sensible oscille, résonne longtemps encore après qu’on l’a pincée. C’est cette oscillation, cette espèce de résonance nécessaire qui tient l’objet présent, tandis que l’entendement s’occupe de la qualité qui lui convient. Mais les cordes vibrantes ont encore une autre propriété, c’est d’en faire frémir d’autres ; et c’est ainsi qu’une première idée en rappelle une seconde, ces deux-là une troisième, toutes les trois une quatrième, et ainsi de suite, sans qu’on puisse fixer la limite des idées réveillées, enchaînées, du philosophe qui médite ou qui s’écoute dans le silence et l’obscurité. Cet instrument a des sauts étonnants, et une idée réveillée va faire quelquefois frémir une harmonique qui en est à un intervalle incompréhensible. Si le phénomène s’observe entre des cordes sonores, inertes et séparées, comment n’aurait-il pas lieu entre des points vivants et liés, entre des fibres continues et sensibles ?... L’analogie, dans les cas les plus composés, n’est qu’une règle de trois qui s’exécute dans l’instrument sensible. Si tel phénomène connu en nature est suivi de tel autre phénomène connu en nature, quel sera le quatrième phénomène conséquent à un troisième, ou donné par la nature, ou imaginé à l’imitation de la nature ? Si la lance d’un guerrier ordinaire a dix pieds de long, quelle sera la lance d’Ajax ? Si je puis lancer une pierre de quatre livres, Diomède doit remuer un quartier de rocher. Les enjambées des dieux et les bonds de leurs chevaux seront dans le rapport imaginé des dieux à l’homme. C’est une quatrième corde harmonique et proportionnelle à trois autres dont l’animal attend la résonance qui se fait toujours en lui-même, mais qui ne se fait pas toujours en nature. Peu importe au poète, il n’en est pas moins vrai. C’est autre chose pour le philosophe ; il faut qu’il interroge ensuite la nature qui, lui donnant souvent un phénomène tout à fait différent de celui qu’il avait présumé, alors il s’aperçoit que l’analogie l’a séduit. »
Maurice Jacob dans « Au cœur de la matière » :
« Une résonance est un phénomène bien connu en physique. Un objet peut vibrer sur une fréquence particulière. L’exemple le plus connu est le pendule qui, suspendu dans le champ d’attraction terrestre, bat à une fréquence qui ne dépend que de sa longueur. Une masse attachée à un ressort se comporte de la même façon. Elle vibre naturellement à une fréquence qui dépend de la valeur de la constante de rappel du ressort. Il en est de même d’un circuit élémentaire de radio. La fréquence naturelle dépend dans ce cas de la self et de la capacité du condensateur qui le constituent. Soumis à une force extérieure périodique, pour le système masse-ressort, ou à une tension périodique, pour le circuit self-capacité, ces systèmes oscillent selon la variation de la force ou de la tension appliquée mais, si la fréquence s’approche de leur fréquence naturelle d’oscillation, ils s’emballent et les oscillations prennent des amplitudes énormes. Quiconque a utilisé une balançoire a pu expérimenter le phénomène. On dit qu’il y a « résonance. »
La résonance est une propriété des oscillateurs couplés, c’est-à-dire de phénomènes périodiques qui parviennent spontanément à augmenter leurs effets en agissant au même rythme.
Ce qui est rythmique est un oscillateur : il dépend de trois éléments, la fréquence, l’amplitude et la phase.
Par exemple, la balançoire, fréquemment citée comme exemple d’oscillateur, a un mouvement périodique dont on peut visualiser aisément la fréquence, l’amplitude et la phase.
Mais l’utilisation de la notion d’oscillateur dépasse largement quelques petits exemples de mécanique. Il a été à la base de la découverte par Planck et Einstein des fondements de la Physique quantique en étudiant l’absorption et l’émission de lumière par la matière, puisque c’est en assimilant la lumière et la matière à des oscillateurs que ce domaine des sciences a été découvert.
Il y a deux possibilités pour qu’un phénomène conserve sa périodicité : soit il n’est pas amorti (pas de frottements), soit il est amorti mais aussi entretenu (il reçoit de l’énergie de l’extérieur).
La fréquence est le nombre fois que le phénomène périodique se reproduit par unité de mesure du temps. La période est le temps nécessaire pour revenir à la position de départ). La fréquence est donc l’inverse de la période.
L’amplitude est le niveau quantitatif de l’oscillation maximale.
La phase est le stade instantané du mouvement. La phase indique le retard ou l’avancée du mouvement. Quand deux mouvements interactifs ont accroché leurs périodes, ils peuvent être en phase ou en opposition de phase.
La résonance, qui fonde un très grand nombre de phénomènes d’interaction, est reliée aux corrélations, inattendues, des rythmes des phénomènes d’avantage qu’à leurs attributs physiques. C’est ainsi que sont reliés le photon lumineux et la matière (atome ou particule), la matière et le vide, le corps et le cerveau, les réseaux neuronaux et les événements mentaux. Les systèmes et les lois concernés par la résonance ont une particularité soulignée par le grand physicien Poincaré : la possibilité de sauter, brutalement et de manière inattendue, d’une structure à une autre, complètement nouvelle.
Il y a en effet des rythmes dans la matière aussi bien que dans la lumière. On sait que la matière est quantique et donc aussi ondulatoire que particulaire, donc elle a des fréquences ! En témoignent les fréquences d’ondes que l’on trouve dans l’un comme dans l’autre. Les fentes de Young démontrent que matière et lumière interfèrent avec eux-mêmes. C’est par la résonance entre l’atome et le champ de l’atome que, dès 1928, Dirac avait expliqué l’instabilité des états stationnaires excités, le fait que 1’atome rejoint spontanément son état fondamental en émettant un (ou des) photon(s).
« Le temps et l’éternité » d’Ilya Prigogine et Isabelle Stengers :
« Pour expliquer les transitions électroniques spontanées qui confèrent à tout état excité un temps de vie fini, Dirac avait dû faire l’hypothèse d’un champ induit par l’atome et entrant en résonance avec lui. »
Ces rythmes peuvent entrer en résonance, ce qui veut dire que, lorsque des matières et lumières interagissent, elles vont le faire plus favorablement si leurs fréquences sont identiques ou proportionnelles, dans des proportions simples, qui sont des rapports de petits nombres entiers comme 1/5, 2/3 ou 3/4. Dans ce cas, ces rythmes vont devenir liés et échanger mutuellement de l’énergie, fondant une structure ordonnée qui lie les deux états. La liaison entre matière comme entre matière et lumière est fondée sur de tels échanges d’énergie qui constitue une structure plus stable que leur existence isolée.
Chaque objet possède une fréquence qui lui est propre que l’on appelle « fréquence de résonance ».
L’exemple le plus simple de la résonance est la balançoire. Celle-ci a un certain rythme de mouvement avec une amplitude et une fréquence. Elle va et vient selon un certain rythme. Si la balançoire reçoit une poussée au bon moment et dans le bon sens, l’amplitude de son mouvement va augmenter. Pour cela, il faut qu’elle reçoive de l’énergie au bon moment (de préférence lors de son amplitude extrême et dans la bonne direction, celle de son mouvement spontané). Du coup, le mouvement de la balançoire est favorisé et son amplitude s’accroît. Il peut suffire que ce « coup de main » se produise une fois sur deux, une fois sur trois, etc., pour que l’aide au mouvement joue ainsi un rôle. Il suffit donc que l’ « aide » ait une fréquence proportionnée au mouvement sur lequel elle agit.
Le pendule n’est pas le seul exemple connu. On se souvient des soldats qui ont rompu un pont en marchant au pas au rythme propre du pont. Ou encore de Nikola Tesla qui, en 1898, attacha un petit oscillateur au pilier de fonte central soutenant l’immeuble où se trouvait son laboratoire new-yorkais (imaginez une sorte de petit pendule se balançant et venant frapper le pilier selon une cadence régulière calculée au préalable). Tesla observa la mise en résonance successive de tous les objets de la pièce, un à un, au fur et à mesure que la fréquence augmentait. Mais peu à peu, à l’insu du savant, la vibration de très basse fréquence s’était communiquée au pilier, puis au sous-sol et aux immeubles avoisinants. Ceux-ci se mirent à trembler, des vitres explosèrent, les habitants affolés se ruaient hors des immeubles. Vers la fin du 19ème siècle Nikola Tesla avait émis l’hypothèse que l’ionosphère autour de la terre (partie de l’atmosphère à 60 km au-dessus de nos têtes) jouait comme une caisse de résonance pour l’électromagnétisme de la terre. Ceci fut confirmé et observé en 1960 au travers d’ondes radio-électriques.
La chaleur est donc la part de l’énergie qui peut se changer en un rayonnement dont la fréquence correspond à certains seuils précis qui lui permettent d’entrer en résonance avec les structures de la matière ayant des tailles comparables à la longueur d’onde de cette énergie. Rappelons que le rayonnement n’est plus conçu comme ondulatoire mais comme une dualité onde/corpuscule fondée sur les couples particules/antiparticules du vide fondant les corpuscules dits photons. L’agitation capable de se transformer en photons dont les énergies correspondent aux dimensions des molécules est donc la seule capable de se changer en « chaleur » et c’est loin d’être la totalité de l’agitation interne. Certes, la transmission de chaleur augmente la température mais les deux sont loin d’être identiques, contrairement à ce que croit le sens commun.
On constate d’autres résonances dans les mouvements planétaires comme la résonance entre les mouvements de précession des orbites de la terre et de Mars, comme la résonance entre les mouvements de précession de Mercure, Vénus et Jupiter. La précession est l’un des paramètres caractérisant le mouvement d’une planète. Du coup, il est difficile de dire si une forte augmentation de l’excentricité du mouvement elliptique d’une planète ne serait pas possible dans un intervalle de cent millions d’années, augmentation pouvant donner une énergie suffisante pour que cette planète sorte du système solaire. L’augmentation de l’excentricité du mouvement elliptique peut causer un choc entre deux planètes comme le montrent les extrapolations de calcul effectuées par Laskar dans une simulation sur ordinateur des équations sur dix milliards d’années. Ce seraient également ces mouvements chaotiques causés par des résonances qui expliqueraient la capacité de certaines trajectoires d’entraîner le corps hors du système, expliquant ainsi les trous dans la ceinture de Kirkwood des astéroïdes (un million de blocs rocheux de moins d’un kilomètre de diamètre qui voyagent entre Jupiter et Mars.)
La résonance signifie le retour régulier d’une interaction brutale. C’est un effet d’entraînement équivalent à l’entretien d’un pendule amorti. On se souvient de l’effet chaotique de cette intervention qui transmet de l’énergie de façon ponctuée au pendule : le mouvement devient chaotique et son avenir est imprédictible. On se souvient par exemple de l’encensoir cité au chapitre « Rétroaction du lent et du rapide » de cette étude. C’est le chaos qui permet de synchroniser les rythmes de la matière, que ce soit les horloges des particules (par le chaos quantique du vide), les circuits électroniques et les lasers (signal électrique entrant chaotique), les oscillations chimiques (comme la glycolyse responsable du principal mode de production d’énergie des cellules vivantes ou les rythmes cardiaques des animaux (chaos causé par la rétroaction des cellules pace-makers du cœur). La raison de cette capacité des messages chaotiques de piloter un système à grande échelle appelée « la maîtrise du chaos » par William Ditto et Louis Pecora, qui écrivent que « Si deux systèmes sont lâchés en opposition de phase, ils le restent pour toujours. (...) En changeant, le signal d’entraînement en un certain type de signal chaotique, deux systèmes peuvent fonctionner en phase. » Cette capacité des résonances au sein du désordre de coordonner les rythmes est une propriété fondamentale du chaos déterministe. Aucune loi non chaotique ne permet à deux ou à un grand nombre de rythmes de s’accrocher ainsi.
Dans toutes les dynamiques produisant des résonances, Poincaré a montré que se retrouvaient des phénomènes du même type (les trajectoires stables sont imbriquées à l’infini dans les trajectoires instables comme dans l’exemple de la dynamique en selle de cheval ou en col) que nous avons appelé « le chaos déterministe ». Dans d’autres domaines que la physique, cette notion allait se révéler productive. La théorie du chaos déterministe a montré d’autre part que des lois peuvent produire des sauts entre des valeurs (discontinuité) et des apparences ressemblant considérablement à du pur hasard. Par exemple, le biologiste Robert May démontrait que, pour certaines valeurs des conditions initiales, une dynamique apparemment régulière autrement, se met à sauter d’une valeur à une autre sans la moindre prédictibilité. Etudiant l’évolution d’une population animale d’une saison à l’autre représentée sous la forme de l’itération d’une suite du type k fois x fois (1-x) et démontrait que, malgré le caractère mathématiquement simple de la fonction, l’itération avec un temps discontinu entraînant une grande complexité des résultats. Et il élargissait ce résultat à d’autres domaines : « Non seulement en recherche, mais aussi dans le monde quotidien de la politique et de l’économie, il serait bénéfique pour tous si plus de gens réalisaient que les systèmes non linéaires simples ne possèdent pas nécessairement des propriétés dynamiques simples. »
De telles résonances peuvent se produire entre une structure et une vibration, si les deux ont des dimensions et des longueurs d’onde proches ou proches d’une proportion simple. C’est le cas, par exemple, entre matière et lumière (on entend par lumière tout phénomène électromagnétique), si la matière a des dimensions caractéristiques (celles des molécules ou celles de la structure cristalline) proches ou proches de la proportion simple par rapport à la longueur d’onde de la lumière.
Il peut également y avoir résonance sans interaction, par exemple entre deux vibrations qui, si elles se produisent à bonne périodicité et phase, additionnent leurs effets périodiquement, additionnent donc leurs énergies et peuvent aller au-delà de l’effet de chacune d’elles.
Un système susceptible d’entrer en résonance, c’est-à-dire susceptible d’être le siège d’oscillations amorties, est un oscillateur. Un tel système a la particularité de pouvoir emmagasiner temporairement de l’énergie sous deux formes : potentielle ou cinétique. L’oscillation est le phénomène par lequel l’énergie du système passe d’une forme à l’autre, de façon périodique.
Par exemple, dans un système mécanique, l’énergie passe de la forme potentielle à la forme cinétique : une corde vibrante aura son énergie sous forme entièrement potentielle au moment où elle passe par son maximum d’élongation. Au moment où la corde passe par sa position d’équilibre, sa vitesse est maximale, et son énergie est entièrement sous forme cinétique.
Dans un circuit RLC, l’énergie est sous forme potentielle quand la tension est maximale aux bornes du condensateur. L’énergie est sous forme cinétique (ou magnétique) quand le courant est maximum dans la bobine (et la tension nulle sur le condensateur).
Si on injecte une énergie potentielle au moment où l’énergie potentielle déjà emmagasinée est maximale, l’énergie ainsi injectée s’ajoute à l’énergie déjà emmagasinée et l’amplitude de l’oscillation va augmenter, ainsi que l’énergie totale. De la même façon, si on injecte de l’énergie cinétique au moment où l’énergie cinétique est maximale, l’énergie totale augmentera. Si on apporte ainsi de l’énergie avec une périodicité égale (ou proche) de la périodicité propre du système, l’énergie totale va augmenter régulièrement. L’amplitude des oscillations du système va ainsi croître. L’exemple le plus simple est celui d’une balançoire : l’énergie de chaque poussée s’ajoute à l’énergie totale, à condition de pousser au bon moment...
Le phénomène de résonance n’est rien d’autre que cet effet d’accumulation de l’énergie en injectant celle-ci au moment où elle peut s’ajouter à l’énergie déjà accumulée, c’est-à-dire « en phase » avec cette dernière.
"Entre le temps et l’éternité" de Prigogine et Stengers :
« La raison du chaos quantique est l’apparition des résonances. (...) Ces résonances, qui caractérisent l’ensemble des situations fondamentales de la mécanique quantique, correspondent à des interactions entre champs (c’est-à-dire aussi aux interactions matière-lumière). On peut affirmer que notre accès au monde quantique a pour condition l’existence des systèmes chaotiques quantiques… en 1892, Poincaré montra qu’en général il est impossible de définir la transformation unitaire qui ferait des « actions » des invariants du système. La plupart des systèmes dynamiques n’admettent pas d’invariants en dehors de l’énergie et de la quantité de mouvement, et dès lors ne sont pas intégrables. La raison de l’impossibilité de définir les invariants du mouvement qui correspondent à la représentation d’un système dynamique intégrable tient à un mécanisme de résonance. (…) Le mécanisme de résonance peut être caractérisé comme un transfert d’énergie entre deux mouvements périodiques couplés dont les fréquences sont entre elles dans un rapport simple. Ce sont ces phénomènes de résonance – mais, cette fois, entre les différents degrés de liberté qui caractérisent un même système dynamique – qui empêchent que ce système soit mis sous une forme intégrable. La résonance la plus simple entre les fréquences se produit quand ces fréquences sont égales, mais elle se produit aussi à chaque fois que les fréquences sont commensurables, c’est-à-dire chaque fois qu’elles ont entre elles un rapport rationnel. Le problème se complique du fait que de manière générale les fréquences ne sont pas constantes. (…) Ce qui fait que, dans l’espace des phases d’un système dynamique, il y aura des points caractérisés par une résonance, alors que d’autres ne le seront pas. L’existence des points de résonance interdit en général la représentation en termes de variables cycliques, c’est-à-dire une décomposition du mouvement en mouvements périodiques indépendants. Les points de résonance, c’est-à-dire les points auxquels les fréquences ont entre elles un rapport rationnel, sont rares, comme sont rares les nombres rationnels par rapport aux nombres irrationnels. Dès lors, presque partout dans l’espace des phases, nous aurons des comportements périodiques de type habituel. Néanmoins, les points de résonance existent dans tout le volume fini de l’espace des phases. D’où le caractère effroyablement compliqué de l’image des systèmes dynamiques telle qu’elle nous a été révélée par la dynamique moderne initiée par Poincaré et poursuivie par les travaux de Kolmogoroff, Arnold et Moser. Si les systèmes dynamiques étaient intégrables, la dynamique ne pourrait nous livrer qu’une image statique du monde, image dont le mouvement du pendule ou de la planète sur sa trajectoire képlérienne constituerait le prototype. Cependant l’existence des résonances dans les systèmes dynamiques à plus de deux corps ne suffit pas pour transformer cette image et la rendre cohérente avec les processus évolutifs étudiés précédemment. Lorsque le volume reste petit, ce sont toujours les comportements périodiques qui dominent. (…) Cependant, pour les grands systèmes, la situation s’inverse. Les résonances s’accumulent dans l’espace des phases, elles se produisent désormais non plus en tout point rationnel, mais en tout point réel. (…) Dès lors, les comportements non périodiques dominent, comme c’est le cas dans les systèmes chaotiques. (…) Dans le cas d’un système de sphères dures en collision, Sinaï a pu démontrer l’identité entre comportement cinétique et chaotique, et définir la relation entre une grandeur cinétique comme le temps de relaxation (temps moyen entre deux collisions) et le temps de Lyapounov qui caractérise l’horizon temporel des systèmes chaotiques. (…) Or, l’atome en interaction avec son champ constitue un « grand système quantique » auquel, nous l’avons démontré, le théorème de Poincaré peut être étendu. (…) La « catastrophe » de Poincaré se répète dans ce cas : contrairement à ce que présupposait la représentation quantique usuelle, les systèmes caractérisés par l’existence de telles résonances ne peuvent être décrits en termes de superposition de fonctions propres de l’opérateur hamiltonien, c’est-à-dire d’invariants du mouvement. Les systèmes quantiques caractérisés par des temps de vie moyens, ou par des comportements correspondants à des « collisions », constituent donc la forme quantique des systèmes dynamiques au comportement chaotique (…) L’abandon du modèle des systèmes intégrables a des conséquences aussi radicales en mécanique quantique qu’en mécanique classique. Dans ce dernier cas, il impliquait l’abandon de la notion de point et de loi d’évolution réversible qui lui correspond. Dans le second, il implique l’abandon de la fonction d’onde et de son évolution réversible dans l’espace de Hilbert. Dans les deux cas, cet abandon a la même signification : il nous permet de déchiffrer le message de l’entropie. (…) La collision, transfert de quantité de mouvement et d’énergie cinétique entre deux particules, constitue, du point de vue dynamique, un exemple de résonance. Or, c’est l’existence des points de résonance qui, on le sait depuis Poincaré, empêche de définir la plupart des systèmes dynamiques comme intégrables. La théorie cinétique, qui correspond au cas d’un grand système dynamique ayant des points de résonance « presque partout » dans l’espace des phases , marque donc la transformation de la notion de résonance : celle-ci cesse d’être un obstacle à la description en termes de trajectoires déterministes et prédictibles, pour devenir un nouveau principe de description, intrinsèquement irréversible et probabiliste. C’est cette notion de résonance que nous avons retrouvée au cœur de la mécanique quantique, puisque c’est elle qu’utilisa Dirac pour expliquer les événements qui ouvrent un accès expérimental à l’atome, l’émission et l’absorption de photons d’énergie spécifique, dont le spectre constitue la véritable signature de chaque type d’atome. (…) Le temps de vie, qui caractérise de manière intrinsèque un niveau excité, dépend, dans le formalisme actuel de la mécanique quantique, d’une approximation et perd son sens si le calcul est poussé plus loin. Dès lors, la mécanique quantique a dû reconnaître l’événement sans pouvoir lui donner de sens objectif. C’est pourquoi elle a pu paraître mettre en question la réalité même du monde observable qu’elle devait rendre intelligible. (…) Pour expliquer les transitions électroniques spontanées qui confèrent à tout état excité un temps de vie fini, Dirac avait dû faire l’hypothèse d’un champ induit par l’atome et entrant en résonance avec lui. Le système fini que représente l’atome isolé n’est donc qu’une abstraction. L’atome en interaction avec son champ est, lui, un « grand système quantique », et c’est à son niveau que se produit la « catastrophe de Poincaré ». L’atome en interaction avec le champ qu’il induit ne constitue pas, en effet, un système intégrable et ne peut donc pas plus être représenté par l’évolution de fonction d’onde qu’un système classique caractérisé par des points de résonance ne peut être caractérisé par une trajectoire. C’est là la faille que recélait l’édifice impressionnant de la mécanique quantique. (…) Il est significatif que, partout, nous ayons rencontré la notion de « brisement de symétrie ». Cette notion implique une référence apparemment indépassable à la symétrie affirmée par les lois fondamentales qui constituent l’héritage de la physique. Et, en effet, dans un premier temps, ce sont ces lois qui ont guidé notre recherche. (…) La description à symétrie temporelle brisée permet de comprendre la symétrie elle-même comme relative à la particularité des objets autrefois privilégiés par la physique, c’est-à-dire de situer leur particularité au sein d’une théorie plus générale. »
Richard Feynman dans son « Cours de Physique – Mécanique 1 » :
« Si nous maintenons un pendule à l’extrémité d’un fil et si nous le secouons à la bonne fréquence, nous pouvons le faire se balancer extrêmement haut… L’importance des phénomènes de résonance réside dans le fait qu’ils se manifestent dans de très nombreuses circonstances… En mécanique, on trouvera que la fréquence de résonance a un carré égal à la rigidité divisée par la masse et en électricité le carré de la fréquence de résonance est l’inverse du produit de L (inductance) et C (capacité électrique)… Les applications de la résonance les plus simples et les plus étendues d’un point de vue technique se trouvent en électricité… On trouve des exemples dans de nombreux domaines et on peut montrer à chaque fois que l’équation de résonance se retrouve être la même. Il y a de nombreuses circonstances dans la nature dans lesquelles quelque chose « oscille », et qui donnent lieu à des phénomènes de résonance… Les deux premiers exemples viennent de la mécanique, le premier sur une grande échelle : l’atmosphère de toute la Terre. Si l’atmosphère que nous supposons entourer la terre uniformément de tous les côtés est tirée d’un côté par la lune, ou plutôt s’écrase en s’allongeant pour former une double marée, et si nous pouvions ensuite la laisser partir, elle se mettrait à osciller ; c’est un oscillateur. Cet oscillateur est couplé à la lune qui tourne effectivement autour de la terre… La réponse de l’atmosphère de la terre à l’attraction de la lune est celle d’un oscillateur…
Nous descendons maintenant à une petite échelle. Cette fois-ci nous prenons un cristal de chlorure de sodium, qui contient des ions sodium et des ions chlore proches les uns des autres. Ces ions sont alternativement chargés électriquement plus et moins. On peut avoir dans ce cas une intéressante oscillation. Supposez que nous puissions écarter toutes les charges positives vers la droite et toutes les charges négatives vers la gauche, et que nous les laissons aller ; elles se mettraient alors à osciller, le réseau de sodium se déplaçant par rapport au réseau de chlore. Comment pouvons-nous réaliser une telle chose ? C’est facile, car si nous appliquons un champ électrique sur le cristal, il va pousser les charges plus dans un certain sens et les charges moins dans l’autre sens ! Ainsi en ayant un champ électrique externe nous pouvons peut-être faire en sorte que le cristal oscille. La fréquence du champ électrique nécessaire est si élevée, cependant, que cela correspond à des rayons infra-rouge ! (…)
Nous passons maintenant à l’exemple de l’oscillation d’un aimant. Si nous plaçons un aimant, avec des pôles Nord et Sud, dans un champ magnétique constant, l’extrémité N sera tirée dans un sens et l’extrémité S dans l’autre sens, et un couple s’exerce en général sur l’aimant, de telle sorte qu’il va vibrer autour de sa position d’équilibre, comme une aiguille de boussole.
Cependant, les aimants dont nous parlons sont les atomes. Ces atomes ont un moment cinétique, le couple ne produit pas un simple mouvement dans la direction du champ, mais au lieu de cela produit, bien sûr, une précession. En la regardant de côté, n’importe quelle composante « oscille », et nous pouvons perturber et entretenir cette oscillation et mesurer une absorption….
Nous allons encore plus loin. Notre exemple suivant se rapporte aux noyaux atomiques. Les mouvements des neutrons et des protons dans les noyaux sont d’une certaine manière oscillants, et nous pouvons démontrer ceci par l’expérience suivante. Nous bombardons un atome de lithium avec des protons, et nous découvrons qu’une certaine réaction, produisant des rayons gamma, a en réalité un maximum très aigu, typique de la résonance. »
« Du vide à l’univers » de Edgar Gunzig, article de l’ouvrage collectif « Le vide » :
« Le face-à-face de la gravitation classique et du monde quantique s’exprime réellement dans ce qu’il a de plus spécifique les liens intimes qu’entretiennent la géométrie de l’espace-temps et les fluctuations du vide, la réponse de l’espace-temps classique à l’univers fluctuant du vide quantique…La géométrie, qui s’était déjà dynamisée en géométrie générale, devient, au terme de ce face-à-face avec la théorie quantique des champs, un partenaire énergétique. La géométrie entre en résonance avec le vide quantique et fluctue classiquement en réponse avec ses fluctuations quantiques. »
« L’objet quantique » de Lochak, Diner et Farge :
« Dans son état de repos, on peut dire que les électrons de l’atome gravitent autour du noyau de sorte que leur onde associée soit en quelque sorte que leur onde associée soit en quelque sorte « accordée » sur l’un des modes de résonance de l’atome. Si une onde électromagnétique tombe alors sur cet atome, elle va faire vibrer ces électrons autour de ce mouvement stationnaire.
Dans le cas général, fréquence de l’onde quelconque, cette vibration va garder la même fréquence et avoir une amplitude assez faible, proportionnelle à celle de l’onde incidente. On a affaire à ce que l’on appelle une oscillation forcée.
Or, l’électron est une particule chargée d’électricité, il va donc se comporter comme une petite antenne et rayonner lui aussi dans toutes les directions une onde électromagnétique de même fréquence. C’est ce qu’on appelle une « diffusion » parce que la lumière va non seulement être transmise dans la direction du faisceau incident, mais aussi être réémise de tous les côtés. C’est, à l’échelle atomique, le même phénomène que celui qui nous permet de voir les rayons du soleil diffusés par la fumée ou la brume.
Si la lumière a une couleur bien déterminée, celle-ci ne changera pas, mais comme l’amplitude diffusée dépend de la fréquence de l’onde, la répartition spectrale d’une lumière blanche, polychromatique, va varier. Dans le domaine visible, ce sont les radiations de courte longueur d’onde qui sont ainsi favorisées. Ceci explique par exemple la couleur bleue du ciel, due à la diffusion de la lumière blanche émise par le soleil par les molécules de la haute atmosphère. Sans diffusion notre ciel serait noir comme celui de la lune qui n’a pas d’atmosphère.
Mais ce phénomène n’est pas à proprement parler quantique. Ce qui l’est, c’est ce qui se passe pour les fameuses fréquences qui correspondent aux raies d’absorption ou d’émission de l’atome. Dans ce cas il y a résonance entre l’onde incidente et le mouvement des électrons. Un exemple tiré de l’expérience courante permet de le comprendre.
Considérons le mouvement d’une balançoire. Si on veut en augmenter l’amplitude, on sait qu’il est inutile de faire un effort violent, et qu’il suffit de quelques coups donnés au bon moment (quand le siège commence juste à redescendre) et répétés bien régulièrement, en synchronisme avec le mouvement pour y arriver.
On voit bien quelles sont les deux conditions pour un bon transfert d’énergie entre l’extérieur et le système oscillant :
1) avoir la même fréquence
2) synchroniser les impulsions pour qu’elles arrivent au bon moment.
Dans ce cas l’amplitude croît régulièrement, et peut même devenir catastrophique, jusqu’à faire complètement changer l’allure du mouvement : de simplement oscillant avec des allers-retours, le balancement peut se transformer en révolutions complètes (tours complets).
C’est un phénomène analogue qui se passe dans un atome. Pour certaines fréquences privilégiées de l’onde incidente, le mouvement de l’électron « décroche » de l’état stationnaire où il se trouvait, son amplitude croît énormément, puis se stabilise à nouveau sur un autre régime stationnaire, de plus haute énergie. Il y a cependant des différences frappantes avec le mouvement classique de la balançoire.
Tout d’abord les fréquences caractéristiques ne sont pas celles qu’on pourrait éventuellement attribuer au mouvement de l’électron. D’une façon tout à fait étrange, et caractéristique de la théorie quantique, elles sont seulement liées aux différences d’énergie entre deux états stationnaires par l’intermédiaire de la loi de Bohr :
E2 – E1= h fois la fréquence nu
dans laquelle E2 – E1 est la différence d’énergie entre les deux états stationnaires, h est la constante de Planck et nu la fréquence du rayonnement ainsi absorbé.
D’autre part, cette même relation montre que, comme l’énergie se conserve, l’électron ne peut pas absorber n’importe quelle quantité d’énergie, mais seulement h fois nu, ce que Planck appelait justement un « quantum » d’énergie, en langage moderne un « photon ».
Reprenons l’image de la balançoire. Si, au lieu d’accentuer son mouvement, on veut au contraire le diminuer, il ne faut pas essayer de s’y opposer d’un coup, ce qui nécessite un effort extrêmement violent, mais il vaut mieux donner une série de petites impulsions de freinage un tout petit peu avant que la balançoire ne passe par le sommet de sa trajectoire. Encore une fois ceci nécessite de synchroniser ces impulsions avec le mouvement, mais cette fois-ci à un instant légèrement différent du précédent. On voit que suivant les cas le même type d’action peut aussi bien s’opposer au mouvement que le favoriser.
Il se passe la même chose dans le monde atomique. Supposons que l’électron atomique soit dans un état de grande énergie, qu’on appelle état « excité ». Il arrive parfois qu’une onde électromagnétique incidente, à condition qu’elle soit accordée sur la bonne fréquence de transition, celle qui est donnée par la loi de Bohr, mette en mouvement l’électron et le fasse à nouveau décrocher, mais cette fois-ci en perdant de l’énergie. Il passe alors sur un « niveau inférieur », état de moindre énergie. Afin de conserver l’énergie, il aura bien entendu cédé à l’onde un photon d’énergie h fois nu. Ce dernier, par le processus même qui a présidé à sa formation, a une propriété remarquable : il est en phase avec l’onde incidente. »
De multiples cas de résonance :























Messages
1. Résonance et rythmologie de la matière/lumière, 9 septembre 2021, 06:37, par A.M.
Résonance de pendules
https://www.canal-u.tv/video/sillages/resonance_de_pendules.13233