Home > 02 - Livre Deux : SCIENCES > Coeur, cerveau et rythmes biologiques > Rythmes auto-organisés > Periodic Stimulation of Biological Oscillators
Periodic Stimulation of Biological Oscillators
Saturday 9 November 2019, by
Synchronization and Rhythmic Processes in Physiology
Multiple Oscilators Provide Metastblity in Rhythm
Phase-locking

Zones of phase locking
Respiratory System

Cardiac Phase-locked Rhythms
Cardiac Phase Resetting

Phase-locking in Parasystole Rhythms

Van der Pol Oscillator

Phase-locking of the van der Pol Oscillator

Dynamical Features od Neurons and the Brain
Periodic Stimulation of Biological Oscillators
Periodic stimulation of spontaneously oscillating physiological rhythms has powerful effects on the intrinsic rhythm. As the frequency and amplitude of the periodic stimulus are varied, a variety of different coupling patterns are set up between the stimulus and the spontaneous oscillator. In some situations the spontaneous rhythm is entrained or phase locked to the forcing stimulus so that for each N cycles of the stimulus there are M cycles of the spontaneous rhythm, and the spontaneous oscillation occurs at fixed phase (or phases) of the periodic stimulus (N:M phase locking). In addition to phase-locked rhythms, it is also possible to observe irregular or aperiodic rhythms in which fixed phase relationships and regular repeating cyclic patterns are not observed. We will discuss the main experimental observations in phase locking experiments, with particular reference to experiments on the cardiac and respiratory systems. We will develop the mathematical concepts needed to analyse phase locking in integrate and fire models and in limit cycle models. We will discuss several phenomena entailing phase locking in humans.
One experimental paradigm for studying physiological oscillators is to subject the oscillator to periodic stimuli while maintaining physiological conditions as constant as possible. We do not attempr to give a complete summary of this large body of work but discuss two illustrative systems: the mechanical ventilation of animals, and the periodic stimulation of cardiac oscillations using an intracellular microelectrode. We draw generalizations from these systems which are broadly applicable in a wide variety of experimental systems.
It has been known since the time of Hering and Breuer that periodic lung inflation by a mechanical ventilator can lead to phase locking between the ventilator and the intrinsic respiratory rhythm in mammals. The entrainment is believed to be mediated by the Hering-Breuer reflexes in which expansion of the lungs inhibits inspiration ans prolongs expiration. Afferent activity from stretch receptors in the lungs is carried by afferent fibers in the vagus nerve. Respiratory entrainment can be studied by mechanically ventilating an animal at different volume and frequencies while attempting to maintain constant levels of anesthesia, body temperature, and blood gases.
Experiments were performed on paralyzed, pentobarbital-anesthetized adult cats, and central respiratory activity was monitored by recording from a branch of the phrenic nerve. In a normal unparalyzed animal, the phrenic nerve nerve innervates the diaphragm, and phrenic nerve activity causes the diaphragm to contract, thus leading to inspiration. In the paralyzed animal, neuromuscular transmission between the phrenic nerve and the diaphragm is blocked, and lung inflation is due solely to the mechanical ventilator. However, afferent activity from stretch receptors in the lung is still carried by the vagus nerve…
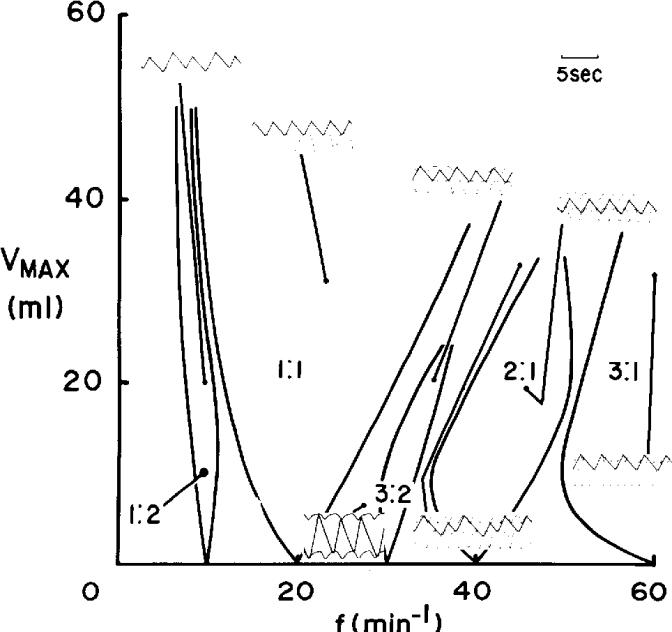
As the ventilator volume and frequency are varied, a number of different rhythms are established between the ventilator and phrenic activity. These different rhythms are organized in an orderly fashion in the ventilator volume-ventilator frequency plane. Insets show representative traces of ventilator volumes and phrenic nerve activity corresponding to different stable phase-locked rhythms, as well as non-phase-locked rhythms (which occur in the shaded regions). In these experiments, low ventilation must be maintained. Likewise, very high volumes and frequencies could not be studied because of the mechanical limitations of the ventilator and the limited lung capacity of the cat.
The respiratory rhythm is generated in a complex network of neurons in the brain stem. In contrast, the cardiac rhythm is generated in a specialized region of electrically coupled cells in the SA node that act as a pacemaker for the heart. We now describe experiments in which the effects of pulsatile electrical stimuli delivered to spontaneously beating cells derived from the ventricles of embryonic chick heart were determined.
As the frequency and current intensity of the electrical stimuli are varied, a variety of different rhythms between the stimulator and the heart cells are established… The insets represent the different observed phase-locking patterns, and the solid lines represent the results of theoretical computations based on phase-resetting experiments using single pulses. In addition to the stable phase-locked rhythms, there are a number of irregular rhythms…
Although thses results have been obtained from two very different physiological systems using different types of periodic stimulation, there are certain striking features common to both. The following generalizations are applicable to a large number of experiments of periodic forcing of biological oscillators.
1. The stable zones of phase locking most commonly observed correspond to low-order ratios between the number of cycles of the forcing stimulus and the intrinsic rhythm (i.e., 2:1 , 3:2 , 1:1 , 2:3 , 1:2). Although other N:M ratios with larger values of N and M can also be observed, these occupy smaller areas in the frequency- amplitude parameter space, and they are consequently easily overlooked or obscured by noise.
2. The stable rhythms are organized in the frequency-amplitude plane in an orderly fashion. It is common to associate a rotation number p = M/N with an N:M rhythm. Then, as the stimulation frequency increases at fixed stimulus amplitude, p decreases.
3. At very low stimulation amplitudes, it is difficult to maintain stable phase locking.
4. If the regions of frequency-amplitude parameter space between stable phase-locking zones are studied, then it is generally possible to find stimulation parameters that give rise to irregular dynamics.
Despite their similarities, there are differences between the cardiac and respiratory systems. For example, the 2:2 region observed in the periodically stimulated cardiac cells was not observed in the mechanically ventilated cats. The goal of theoretical studies of phase locking is to provide a theoretical basis for understanding the similarities and differences between the different preparations. Ideally, one would like to be able to make predictions about the phase locking as stimulation parameters vary, based on the mechanisms of rhythmogenesis and the coupling of the stimulator to the intrinsic rhythm. In practice, the mechanical analysis of periodically forced nonlinear oscillators is an extremely difficult problem, and detailed quantitative understanding of dynamics has been obtained in only a few special situations.
The theoretical studies make it clear that although there are many similarities between the dynamics in different systems, there will also generally be differences if the dynamics are studied in sufficient detail. In order to establish this assertion, we describe the dynamics resulting from periodic stimulation in a number of different model systems. We also discuss entrainment of biological oscillators in a number of clinical contexts. (…)
One motivation for the analysis of periodic forcing of integrate and fire models comes from the experimental studies on the mechanical ventilation of cats. An examination of the insets, in particular the 1:2 and 3:2 rhythms, shows large lung inflations coincident with the premature termination of the inspiratory activity. This gives a striking visual suggestion for the utility of an integrate and fire model with modulated threshold for this system. As we already discussed, the Hering-Breuer reflexes can be modeled by integrate and fire models. (…)
In addition to studies of integrate and fire models in which the thresholds are sinusoidal, there have been several studies of the properties of integrate and fire models in which the thresholds are piecewise linear. Such studies allow a much more complete analysis of the dynamics than is possible using sinusoidal thresholds. For example, Lasota and Mackey proved that such models display chaotic dynamics in some parameter ranges. The significance of this finding lies in the observation of chaos even in extremely simplified models for the periods forcing of oscillations. In view of this finding, it seems likely that the appearance of chaotic dynamics at least over some range of stimulation parameters in periodically forced physiological oscillators may be very common.
Attemps to develop more realistic integrate and fire models for the entrainment of the respiratory rhythm have been made by Petrillo and Glass. They assume that two thresholds are modulated by the volume of the mechanical ventilator. The timing of inspiration and expiration is represented by activities that oscillate between the two thresholds. A brief delay occurs between the time the inspiratory onset threshold was reached and the beginning of inspiration. This model has five parameters, all of which could be determined from the data. Numerical simulations of the model show good agreement with the experimental results. However, a detailed study of the bifurcations in this model was not carried through.
Another attempt to develop integrate and fire models for the entrainment of biological rhythms was made by Daan and coworkers for the circadian rhythm. They assumed that there were two sinusoidally modulated thresholds. With this model they were able to provide a partial explanation for data on sleep duration as a function of the time of onset entrainment (corresponding to the normal circadian rhythm), or of other possible phase-locking zones as a function of the parameters.
In conclusion, the assumption that there are periodic inputs to integrate and fire models provides a conceptually simple means to model phase locking in biological systems. Even the simplest possible models lead to extremely complicated dynamics, which are only partially understood.
Many biological rhythms are best represented mathematically as limit cycle oscillations in differential equations. Because these rhythms interact with each other and because there is a periodic stimulation from the external environment, it is important to understand the effects of periodic forcing on a limit cycle oscillation. One prototypical model for periodically forced limit cycles is the sinusoidally forced van der Pol equation. J.H. Jensen and coworkers have shown that sinusoidal forcing also gives rise to chaotic dynamics in mathematical models of excitable neural and cardiac tissue, and Aihara and coworkers have demonstrated strange attractors from sinusoidally forced squid axons.
We now consider the effects of a periodic train of short pulsatile stimuli on limit cycle oscillations. In the event that the limit cycle is rapidly restablished following a single stimulus, it is straightforward to compute the effect of periodic stimuli once the effects of a single stimulus are understood.
The main idea can be developed from a consideration of the effects of a periodic stimulation of the Poincaré oscillator...”
Zones of phase locking from Glass and Petrillo (1984)
Theoretically computed phase-locking zones from Glass, Guevara and Shrier (1987)
Regions of phase locking of the van der Pol oscillator from Hayashi (1964)
Theoretical model of phase-locking from Petrillo and Glass (1984)
Phase locking of respiration from Bramble (1983)
Phase-locking zones in a mathematical model of parasystole from Moe et al. (1977)
Phase locked rhythms set up between a mechanical ventilator and the respiratory rhythms in an anesthetized human being from Graves et al. (1986)
Glass-Mackey, « The Rythms of Life »