Henri Poincaré invente le chaos déterministe

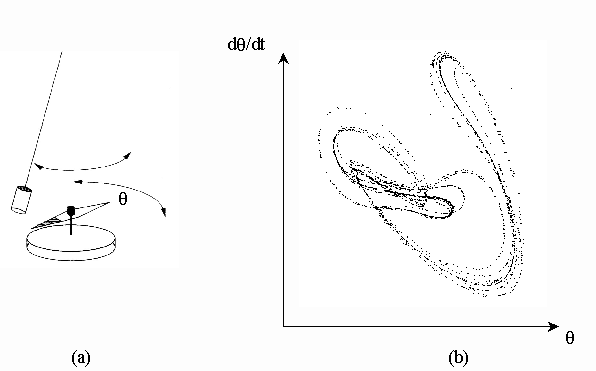
Mouvement d’une boussole devant un pendule métallique

« On sera frappé de la complexité de cette figure, que je ne cherche même pas à tracer. Rien n’est plus propre à nous donner une idée de la complexité du problème des trois corps, et, en général, de tous les problèmes de la dynamique où il n’y a pas d’intégrale uniforme… »

Henri Poincaré
Dans « Méthodes nouvelles de la mécanique céleste »

Quand Henri Poincaré inventait le chaos déterministe

Extrait de « Sciences et méthode » :

« Une cause très petite, qui nous échappe, détermine un effet considérable que nous ne pouvons pas ne pas voir, et alors nous disons que cet effet est dû au hasard. Si nous connaissions exactement les lois de la nature et la situation de l’univers à l’instant initial, nous pourrions prédire exactement la situation de ce même univers à un instant ultérieur. Mais, lors même que les lois naturelles n’auraient plus de secret pour nous, nous ne pourrons connaître la situation initiale qu’approximativement. Si cela nous permet de prévoir la situation ultérieure avec la même approximation, c’est tout ce qu’il nous faut, nous disons que le phénomène a été prévu, qu’il est régi par des lois ; mais il n’en est pas toujours ainsi, il peut arriver que de petites différences dans les conditions initiales en engendrent de très grandes dans les phénomènes finaux ; une petite erreur sur les premières produirait une erreur énorme sur les derniers. La prédiction devient impossible et nous avons le phénomène fortuit. »

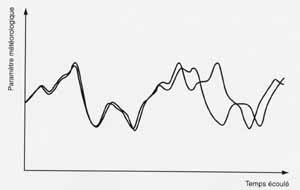
LA "SENSIBILITÉ AUX CONDITIONS INITIALES" SIGNIFIE QUE LES LOIS NE PERMETTENT PAS DE PRÉDIRE PARCE QU’UN TOUT PETIT CHANGEMENT DES VALEURS DE DÉPART ENTRAINE UN AVENIR TRÈS DIFFÉRENT

En 1889, le mathématicien et physicien Henri Poincaré cherchait à répondre à la question de la stabilité du système solaire. Son mémoire intitulé « sur le problème des trois corps et les équations de la dynamique » remporta le prix du concours ouvert à Stockholm par le roi Oscar II entre les mathématiciens du monde entier, apportant à Poincaré une notoriété internationale. Et c’est dans l’étude du système solaire que l’on a découvert pour la première fois un phénomène chaotique ! En effet, il devait montrer que la gravitation avait beau obéir à des lois, celles-ci engendraient le chaos, cette imbrication d’ordre et de désordre que l’on appelle chaos déterministe. Je rappelle que déterministe signifie un phénomène issu de lois. Poincaré a ainsi montré que certaines lois non linéaires, les lois de l’attraction universelle de Newton en l’occurrence, peuvent engendrer des mouvements chaotiques. Poincaré a également montré qu’un mouvement chaotique peut paraître stable durant quelques dizaines ou centaines de millions d’années avant de quitter la zone de stabilité appelée par lui « un îlot » de stabilité. Et pour cette étude il a considérablement simplifié le problème du système solaire. Il a étudié le mouvement de trois corps. Poincaré a ainsi découvert en étudiant mathématiquement la loi de Newton pour ces trois corps qu’on y trouvait des possibilités nombreuses de mouvements imprédictibles. Etonné et en même temps déçu, il aurait déclaré : « si j’avais su qu’en étudiant les lois de la physique on ne pourrait rien prédire, j’aurais préféré me faire boulanger ou postier que physicien et mathématicien ! »

Mais Poincaré avait rapidement compris que ce n’était pas une faiblesse personnelle qui l’empêchait ainsi de pénétrer le fonctionnement de la nature mais une propriété fondamentale de ce fonctionnement et de sa relation avec l’entendement humain. N’oublions pas que Poincaré, même s’il était un grand scientifique, a plutôt souligné le caractère humain et sensible de l’activité intellectuelle de la science. Je le cite commentant l’activité de la découverte scientifique et expliquant qu’entre deux périodes de travail conscient, il se réalise un travail inconscient. « Le moi inconscient ou, comme on dit, le moi subliminal, joue un rôle capital dans l’invention mathématique […] le moi subliminal n’est nullement inférieur au moi conscient ; il n’est pas purement automatique, il est capable de discernement, il a du tact, de la délicatesse ; il sait choisir, il sait deviner…les phénomènes inconscients privilégiés, ceux qui sont susceptibles de devenir conscients, ce sont ceux qui, directement ou indirectement, affectent le plus profondément notre sensibilité. On peut s’étonner de voir invoquer la sensibilité à propos de démonstrations mathématiques qui, semble-t-il, ne peuvent intéresser que l’intelligence. Ce serait oublier le sentiment de la beauté mathématique, de l’harmonie des nombres et des formes, de l’élégance géométrique. C’est un vrai sentiment esthétique que tous les vrais mathématiciens connaissent. » C’est un passage du chapitre « L’invention mathématique », dans l’ouvrage « Science et méthode » de Poincaré.

Et l’un des résultats de ses travaux sera de relativiser le caractère purement objectif des énoncés scientifiques. Il montre que la science reste une conjecture et non un domaine du certain comme on l’a longtemps cru de façon un peu prétentieuse, à la suite de Laplace. Selon lui, la science est une activité humaine et la relation entre l’homme et la nature reste une recherche sans réponse finale. La meilleure preuve en est que ses propres travaux allaient être rapidement contredits puisqu’il concluait que le système solaire était stable ce que, par la suite, il allait lui-même corriger. Par contre, il a inventé à cette occasion la plupart des méthodes théoriques aujourd’hui appliquées dans un domaine qui n’existait pas à l’époque : l’étude des systèmes dynamiques, autrement appelée chaos déterministe. Il écrit : « Une cause très petite qui nous échappe détermine un effet considérable que nous ne pouvons pas ne pas voir et alors nous disons que cet effet est dû au hasard ». C’est la notion de sensibilité aux conditions initiales.

Dans « Science et méthode », Henri Poincaré explique que l’origine de l’apparence de hasard par le caractère des lois universelles pour lesquelles un petit changement peut produire un grand effet. Du coup, il faudrait connaître tous les détails de la situation, à toutes les échelles, pour prédire : « Si nous connaissions exactement les lois de la nature et la situation de l’univers à l’instant initial, nous pourrions prédire la situation de ce même univers à un instant ultérieur. Mais, lors même que les lois naturelles n’auraient plus de secret pour nous, nous ne pourrons connaître la situation initiale qu’approximativement (...). Il peut arriver que des petites différences dans les conditions initiales en engendrent de très grandes dans les phénomènes finaux ; une petite erreur sur les premières produirait une erreur énorme sur les derniers. La prédiction devient impossible et nous avons le phénomène fortuit. » C’est la notion de « sensibilité aux conditions initiales ».

Poincaré va notamment inventer des méthodes d’étude (espace des phases, section de Poincaré, …) de systèmes pris dans leur ensemble sans étudier les éléments du système pris un par un, méthode particulièrement novatrice. Il va étudier non une seule trajectoire mais l’ensemble des trajectoires possibles et leur relation entre elles. Enfin, il va montrer que les phénomènes physiques sont du domaine de la géométrie et non des formules mathématiques. Je le répète, sa conclusion est qu’avec trois corps interagissant par attraction gravitationnelle on a déjà du chaos c’est-à-dire un phénomène obéissant à la propriété de la sensibilité aux conditions initiales : un tout petit changement de celles-ci peut entraîner un grand changement de la suite de l’évolution. Rappelons que cette thèse révolutionne la conception que l’on avait de la gravitation depuis Newton. Ce dernier pensait que si l’on connaissait précisément les positions et les vitesses de tous les corps célestes on pouvait connaître à tout moment la suite des positions. Poincaré infirme cette thèse. Essayons d’expliquer pourquoi. Je vous rappelle que pour deux corps, du moment que l’on connaît la masse des deux corps et les données de position et de vitesse à l’instant initial on peut calculer les positions des deux corps à tout instant. On connaît en effet une solution analytique qui indique le mouvement et il y a une seule trajectoire possible qui est une ellipse.

On pourrait imaginer que l’on est certain d’avoir une solution puisque l’on connaît les équations du mouvement mais ce n’est pas du tout le cas. La plupart des équations mathématiques non linéaires n’ont pas de solution ou une infinité de solutions.

Une solution analytique est une formule qui indiquera positions et déplacements à tout instant. Les équations ne permettent pas de le dire. Les équations de Newton relient par une formule les diverses dérivées de ces quantités, c’est-à-dire position, vitesse et accélération. Lorsque l’on peut revenir des dérivées aux quantités elles-mêmes on dit que le système d’équations est intégrable mais généralement ce n’est pas le cas. Un exemple bien connu d’intégration est l’équation du mouvement d’un boulet de canon si on connaît la vitesse initiale et l’angle de lancement. Et justement dans le cas du système solaire, en se contentant de trois corps, Poincaré a montré que le système n’est pas intégrable. Il n’y a pas de solution analytique des équations de Newton du mouvement. Poincaré en a même expliqué la raison : il n’y a pas assez d’équations par rapport au nombre d’inconnues. Ce que l’on appelle les inconnues ce sont les positions des corps et leurs variations. Les équations indiquent la conservation d’un certain nombre de quantités qui ne peuvent que s’échanger et non diminuer ou augmenter : l’énergie, la quantité de mouvement et la quantité de rotation.

Il a montré que la multiplicité des trajectoires très proches et imbriquées rend improbable que le système soit intégrable. Les équations ne sont pas assez nombreuses pour en déduire une solution. Il a également montré qu’il en découle une infinité de trajectoires possibles et que l’on n’a aucun moyen de trancher entre elles. En plus la proximité des trajectoires signifie qu’une petite perturbation peut faire sauter le corps d’une trajectoire à une autre imperceptiblement avec du coup un avenir tout à fait différent au bout d’un certain temps. Quelle en est la raison ? Dans le mouvement des trois corps, aucun n’est négligeable. A tout instant la position d’un corps et son mouvement sont modifiés par la position précédente d’un autre corps qui est elle-même modifiée par celle du troisième. C’est ce qui rend impossible les approximations. Impossible par conséquent de dire que tel objet est trop petit pour influencer le système sur le long terme. Impossible de dire que telle modification de distance est négligeable puisqu’elle peut entraîner un changement de trajectoire qui peut être considérable sur le long terme. Impossible même de distinguer l’une des planètes comme un objet indépendant du système. Impossible aussi de distinguer passé et présent. En effet, la position d’une planète dépend de l’ensemble des positions précédentes, de toute l’histoire passée du système. C’est ainsi que, pour prédire, il faudrait connaître avec une précision infinie l’ensemble des conditions précédentes et pas seulement les conditions initiales, c’est-à-dire à un instant donné, du système. Du coup, les trajectoires possibles étant infiniment proches les unes des autres, il suffit d’un petit changement dans les conditions initiales ou d’une petite imprécision pour changer relativement vite l’ensemble de l’histoire de tout le système. Poincaré venait de découvrir le premier domaine d’étude d’un phénomène d’un type nouveau : le chaos déterministe.

Parmi les successeurs des travaux de Poincaré, il convient d’abord de citer Kolmogorov, Arnold et Moser. Ces trois scientifiques vont reprendre le travail de Poincaré et montrer en 1962 dans un théorème appelé KAM de leurs initiales que, dans certaines conditions initiales particulières, il peut y avoir stabilité. Il y a alors des mouvements quasi périodiques et des perturbations suffisamment petites ne peuvent éloigner durablement la planète de sa trajectoire.

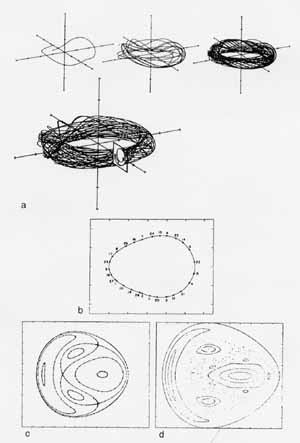
Ils ont donc fait la démonstration que, si les masses et les inclinaisons des ellipses parcourues restent faibles, ces trajectoires restent contraintes à n’évoluer qu’autour d’une espèce de tuyau refermé sur lui-même et appelé le tore. Cette contrainte entraîne une garantie de stabilité, une espèce de garde fou pour le mouvement.
Mais le débat n’était pas achevé pour autant car d’autres physiciens allaient montrer que le théorème KAM s’applique bien à des interactions entre plusieurs corps mais pas au système solaire qui ne satisfait pas aux conditions initiales nécessaires.

Ainsi, en 1998, les savants américains Sussman et Wisdom intègrent le mouvement de Pluton sur un ordinateur et ce mouvement s’avère chaotique. Ils démontrent que ce mouvement obéit à ce que l’on appelle la « sensibilité aux conditions initiales » ou encore la propriété de divergence exponentielle. Exponentielle signifie ici qu’une perturbation au lieu d’additionner ses effets les multiplie et c’est là que réside la source du chaos. En effet, ces deux scientifiques ont calculé que l’incertitude sur les conditions initiales est multipliée par trois tous les 20 millions d’années. Cela signifie qu’en 400 millions d’années, durée sur laquelle on cherche à obtenir une réponse de stabilité, la position de Pluton est complètement imprédictible. L’incertitude est en effet multipliée par trois à la puissance vingt soit 3.486.784.401. Une erreur d’un centimètre se traduit au bout de 400 millions d’années par une modification du résultat de trois milliards et demi de centimètres ! !

Mais c’est surtout dans la foulée des travaux de Jacques Laskar, directeur de recherches au bureau des longitudes de Paris qu’ont été faites les principales découvertes tendant à prouver le caractère chaotique du système solaire. Il a notamment mis en équation le calcul des perturbations qui permet d’extrapoler pour trouver les positions des planètes et il a montré que ce calcul n’était pas valable sur un temps de plusieurs centaines de millions d’années. Les calculs que nous faisons pour positionner les planètes ne sont pas faux mais ils ne sont pas extrapolables pour en déduire la position d’une planète sur une aussi longue durée. La raison ne provient pas d’une erreur ni d’une approximation mais du principe lui-même du calcul. Toute petite approximation entraîne sur un temps aussi long une modification considérable du fait du caractère exponentiel des divergences. Comment ces perturbations peuvent-elles se multiplier ainsi au lieu de simplement s’additionner ? L’explication provient de la rétroaction qui se produit parfois entre deux trajectoires, c’est-à-dire qu’elles ont des fréquences que l’on dit accrochées ou en résonance. Sont en résonance deux phénomènes réguliers dont les périodes sont dans un rapport simple par exemple un sur deux ou trois sur cinq. Dès que deux phénomènes sont dans ce cas, ils interagissent bien plus que la proportion de leur cause. C’est ce qui se produit avec une personne poussant en résonance une balançoire. Cela a pour effet d’accumuler des effets d’entraînement pouvant aller jusqu’au tour complet. Or le rapport entre les périodes des mouvements de Saturne et Jupiter autour du Soleil est exactement dans la fraction 2 sur 5. Cela signifie qu’ils vont se trouver à intervalle régulier dans des positions susceptibles de déformer leurs trajectoires et toujours dans le même sens.

On constate d’autres résonances dans les mouvements planétaires comme la résonance entre les mouvements de précession des orbites de la terre et de Mars, comme la résonance entre les mouvements de précession de Mercure, Vénus et Jupiter. La précession est l’un des paramètres caractérisant le mouvement d’une planète. Du coup, il est difficile de dire si une forte augmentation de l’excentricité du mouvement elliptique d’une planète ne serait pas possible dans un intervalle de cent millions d’années, augmentation pouvant donner une énergie suffisante pour que cette planète sorte du système solaire. L’augmentation de l’excentricité du mouvement elliptique peut causer un choc entre deux planètes comme le montrent les extrapolations de calcul effectuées par Laskar dans une simulation sur ordinateur des équations sur dix milliards d’années. Ce seraient également ces mouvements chaotiques causés par des résonances qui expliqueraient la capacité de certaines trajectoires d’entraîner le corps hors du système, expliquant ainsi les trous dans la ceinture de Kirkwood des astéroïdes (un million de blocs rocheux de moins d’un kilomètre de diamètre qui voyagent entre Jupiter et Mars.)

La résonance signifie le retour régulier d’une interaction brutale. C’est un effet d’entraînement équivalent à l’entretien d’un pendule amorti. On se souvient de l’effet chaotique de cette intervention qui transmet de l’énergie de façon ponctuée au pendule : le mouvement devient chaotique et son avenir est imprédictible. On se souvient par exemple de l’encensoir cité au chapitre « Rétroaction du lent et du rapide » de cette étude. C’est le chaos qui permet de synchroniser les rythmes de la matière, que ce soit les horloges des particules (par le chaos quantique du vide), les circuits électroniques et les lasers (signal électrique entrant chaotique), les oscillations chimiques (comme la glycolyse responsable du principal mode de production d’énergie des cellules vivantes ou les rythmes cardiaques des animaux (chaos causé par la rétroaction des cellules pace-makers du cœur). La raison de cette capacité des messages chaotiques de piloter un système à grande échelle appelée « la maîtrise du chaos » par William Ditto et Louis Pecora, qui écrivent que « Si deux systèmes sont lâchés en opposition de phase, ils le restent pour toujours. (...) En changeant, le signal d’entraînement en un certain type de signal chaotique, deux systèmes peuvent fonctionner en phase. » Cette capacité des résonances au sein du désordre de coordonner les rythmes est une propriété fondamentale du chaos déterministe. Aucune loi non chaotique ne permet à deux ou à un grand nombre de rythmes de s’accrocher ainsi.

Dans toutes les dynamiques produisant des résonances, Poincaré a montré que se retrouvaient des phénomènes du même type (les trajectoires stables sont imbriquées à l’infini dans les trajectoires instables comme dans l’exemple de la dynamique en selle de cheval ou en col) que nous avons appelé « le chaos déterministe ». Dans d’autres domaines que la physique, cette notion allait se révéler productive. La théorie du chaos déterministe a montré d’autre part que des lois peuvent produire des sauts entre des valeurs (discontinuité) et des apparences ressemblant considérablement à du pur hasard. Par exemple, le biologiste Robert May démontrait que, pour certaines valeurs des conditions initiales, une dynamique apparemment régulière autrement, se met à sauter d’une valeur à une autre sans la moindre prédictibilité. Etudiant l’évolution d’une population animale d’une saison à l’autre représentée sous la forme de l’itération d’une suite du type k fois x fois (1-x) et démontrait que, malgré le caractère mathématiquement simple de la fonction, l’itération avec un temps discontinu entraînant une grande complexité des résultats. Et il élargissait ce résultat à d’autres domaines : « Non seulement en recherche, mais aussi dans le monde quotidien de la politique et de l’économie, il serait bénéfique pour tous si plus de gens réalisaient que les systèmes non linéaires simples ne possèdent pas nécessairement des propriétés dynamiques simples. »

Comme l’expose le physicien David Ruelle dans « Où le chaos intervient-il ? », « Le mot chaos fut introduit en 1975 par Jim Jorke, mathématicien à l’Université du Maryland et, vers le milieu des années 1970, le chaos devint une discipline scientifique à part entière. Les nouvelles idées étaient appliquées dans des domaines variés. Robert May, qui travaillait alors au département de zoologie de l’Université de Princeton, montra en 1976 comment le chaos justifie l’existence de fluctuations irrégulières dans les populations animales. En chimie, on savait que certaines réactions étaient oscillantes : je suggérai en 1973 que l’on cherche des oscillations chimiques chaotiques. Plus tard, en effet, on les découvrit et cela a donné, à partir de 1980, à une reconstruction complète de la dynamique des réactions chimiques oscillantes par un groupe de chimistes de l’Université de Bordeaux. Parmi les travaux récents inspirés du chaos, les plus passionnants sont, à mon avis, accomplis en astronomie. Jack Wisdon, de l’Institut de Technologie du Massachussets, Jacques Laskar du Bureau des longitudes de Paris et quelques autres étudièrent, à la lumière de la théorie du chaos, les trajectoires des planètes du système solaire. (...) Il existe en biologie de nombreux phénomènes périodiques d’importance vitale : les rythmes cardiaque, respiratoire, hormonal, entre autres. Il est vraisemblable que la théorie des systèmes dynamiques sera utile pour analyser ces rythmes et quelques résultats appréciables sont déjà apparus, en particulier le travail de Léon Glass à Montréal sur le fonctionnement des cellules cardiaques. » Quelles sont les questions des sciences auxquelles la théorie du chaos offre des approches nouvelles. Je vais en citer quelques unes : l’émergence, l’instabilité dans la stabilité, l’interprétation de la multi-stationnarité (plusieurs états stationnaires possibles avec des sauts de l’un à l’autre), la théorie de la bifurcation (permettant de visionner un changement qualitatif), l’interprétation de l’imprédictibilité de certaines lois non linéaires, etc…"

Extraits de "Entre le temps et l’éternité" de Prigogine et Stengers :

"La raison du chaos quantique est l’apparition des résonances. (...) Ces résonances, qui caractérisent l’ensemble des situations fondamentales de la mécanique quantique, correspondent à des interactions entre champs (c’est-à-dire aussi aux interactions matière-lumière). On peut affirmer que notre accès au monde quantique a pour condition l’existence des systèmes chaotiques quantiques. (...)

« Nous avons surtout souligné les dimensions négatives du chaos dynamique, la nécessité qu’il implique d’abandonner les notions de trajectoire et de déterminisme. Mais l’étude des systèmes chaotiques est également une ouverture ; elle crée la nécessité de construire de nouveaux concepts, de nouveaux langages théoriques. Le langage classique de la dynamique implique les notions de points et de trajectoires, et, jusqu’à présent, nous-mêmes y avons eu recours alors même que nous montrions l’idéalisation – dans ce cas illégitime – dont elles procèdent. Le problème est maintenant de transformer ce langage, de sorte qu’il intègre de manière rigoureuse et cohérente les contraintes que nous venons de reconnaître.
Il ne suffit pas, en effet, d’exprimer le caractère fini de la définition d’un système dynamique en décrivant l’état initial de ce système par une région de l’espace des phases, et non par un point. Car une telle région, soumise à l’évolution que définit la dynamique classique, aura beau se fragmenter au cours du temps, elle conservera son volume dans l’espace des phases. C’est ce qu’exprime un théorème général de la dynamique, le théorème de Liouville. Toutes les tentatives de construire une fonction entropie, décrivant l’évolution d’un ensemble de trajectoires dans l’espace des phases, se sont heurtées au théorème de Liouville, au fait que l’évolution d’un tel ensemble ne peut être décrite par une fonction qui croîtrait au cours du temps.
Or, un argument simple permet de montrer l’incompatibilité, dans le cas d’un système chaotique, entre le théorème de Liouville et la contrainte selon laquelle toute description définit le « pouvoir de résolution » de nos descriptions ; il existera toujours une distance r telle que nous ne pourrons faire de différence entre des points plus proches l’un de l’autre (…) La nouvelle description des systèmes dynamiques chaotiques substitue au point un ensemble correspondant à un fragment de fibre contractante. Il s’agit d’une description non locale, qui tient compte de la contrainte d’indiscernabilité que nous avons définie. Mais cette description n’est pas relative à notre ignorance. Elle donne un sens intrinsèque au caractère fini de nos descriptions : dans le cas où le système n’est pas chaotique, où l’exposant de Lyapounov est de valeur nulle, nous retrouvons la représentation classique, ponctuelle, et les limites mises à la précision de nos mesures n’affectent plus la représentation du système dynamique.
Cette nouvelle représentation brise également la symétrie temporelle. (…) Là où une seule équation d’évolution permettait de calculer l’évolution vers le passé ou vers le futur de points eux-mêmes indifférents à cette distinction, nous avons maintenant deux équations d’évolution différentes. L’une décrirait l’évolution d’un système vers un équilibre situé dans le futur, l’autre décrirait l’évolution d’un système vers un équilibre situé dans le passé.
L’un des grands problèmes de l’interprétation probabiliste de l’évolution vers l’équilibre était que la représentation probabiliste ne donne pas sens à la distinction entre passé et futur. (…) La nouvelle description dynamique que nous avons construite incorpore, en revanche, la flèche du temps (…) Les comportements dynamiques chaotiques permettent de construire ce pont, que Boltzmann n’avait pu créer, entre la dynamique et le monde des processus irréversibles. La nouvelle représentation de l’objet dynamique, non locale et à symétrie temporelle brisée, n’est pas une description approximative, plus pauvre que la représentation classique. Elle définit au contraire cette représentation classique comme relative à un cas particulier. (…) Nous savons aujourd’hui que ces derniers (les systèmes non-chaotiques), qui dominèrent si longtemps l’imagination des physiciens, forment en fait une classe très particulière. (…) C’est en 1892, avec la découverte d’un théorème fondamental par Poincaré ( la loi des trois corps), que se brisa l’image homogène du comportement dynamique : la plupart des systèmes dynamiques, à commencer par le simple système « à trois corps » ne sont pas intégrables.
Comment comprendre cet énoncé ? Depuis les travaux de Hamilton, on sait qu’un même système dynamique peut être représenté de différentes manières équivalentes par une transformation dite canonique (ou unitaire) (…) L’hamiltonien du système est la grandeur qui détermine son évolution temporelle.
Parmi toutes les transformations unitaires, il en existe une qui permet d’aboutir à une représentation privilégiée du système. C’est celle qui fait de l’énergie, c’est-à-dire de l’hamiltonien, une fonction des seuls moments, et non plus des positions. Dans une telle représentation, les mouvements des différentes particules du système sont décrits comme s’ils ne dépendaient plus des positions relatives des particules, c’est-à-dire comme si elles n’étaient plus en interaction. (…) Les mouvements possibles de tels systèmes ont donc la simplicité des mouvements libres. (…)
Or, en 1892, Poincaré montra qu’en général il est impossible de définir la transformation unitaire qui ferait des « actions » des invariants du système. La plupart des systèmes dynamiques n’admettent pas d’invariants en dehors de l’énergie et de la quantité de mouvement, et dès lors ne sont pas intégrables.
La raison de l’impossibilité de définir les invariants du mouvement qui correspondent à la représentation d’un système dynamique intégrable tient à un mécanisme de résonance. (…) Le mécanisme de résonance peut être caractérisé comme un transfert d’énergie entre deux mouvements périodiques couplés dont les fréquences sont entre elles dans un rapport simple.
Ce sont ces phénomènes de résonance – mais, cette fois, entre les différents degrés de liberté qui caractérisent un même système dynamique – qui empêchent que ce système soit mis sous une forme intégrable. La résonance la plus simple entre les fréquences se produit quand ces fréquences sont égales, mais elle se produit aussi à chaque fois que les fréquences sont commensurables, c’est-à-dire chaque fois qu’elles ont entre elles un rapport rationnel. Le problème se complique du fait que de manière générale les fréquences ne sont pas constantes. (…) Ce qui fait que, dans l’espace des phases d’un système dynamique, il y aura des points caractérisés par une résonance, alors que d’autres ne le seront pas. L’existence des points de résonance interdit en général la représentation en termes de variables cycliques, c’est-à-dire une décomposition du mouvement en mouvements périodiques indépendants.
Les points de résonance, c’est-à-dire les points auxquels les fréquences ont entre elles un rapport rationnel, sont rares, comme sont rares les nombres rationnels par rapport aux nombres irrationnels. Dès lors, presque partout dans l’espace des phases, nous aurons des comportements périodiques de type habituel. Néanmoins, les points de résonance existent dans tout le volume fini de l’espace des phases. D’où le caractère effroyablement compliqué de l’image des systèmes dynamiques telle qu’elle nous a été révélée par la dynamique moderne initiée par Poincaré et poursuivie par les travaux de Kolmogoroff, Arnold et Moser.

Si les systèmes dynamiques étaient intégrables, la dynamique ne pourrait nous livrer qu’une image statique du monde, image dont le mouvement du pendule ou de la planète sur sa trajectoire képlérienne constituerait le prototype. Cependant l’existence des résonances dans les systèmes dynamiques à plus de deux corps ne suffit pas pour transformer cette image et la rendre cohérente avec les processus évolutifs étudiés précédemment. Lorsque le volume reste petit, ce sont toujours les comportements périodiques qui dominent. (…)
Cependant, pour les grands systèmes, la situation s’inverse. Les résonances s’accumulent dans l’espace des phases, elles se produisent désormais non plus en tout point rationnel, mais en tout point réel. (…) Dès lors, les comportements non périodiques dominent, comme c’est le cas dans les systèmes chaotiques. (…)
Dans le cas d’un système de sphères dures en collision, Sinaï a pu démontrer l’identité entre comportement cinétique et chaotique, et définir la relation entre une grandeur cinétique comme le temps de relaxation (temps moyen entre deux collisions) et le temps de Lyapounov qui caractérise l’horizon temporel des systèmes chaotiques. (…)
Or, l’atome en interaction avec son champ constitue un « grand système quantique » auquel, nous l’avons démontré, le théorème de Poincaré peut être étendu. (…) La « catastrophe » de Poincaré se répète dans ce cas : contrairement à ce que présupposait la représentation quantique usuelle, les systèmes caractérisés par l’existence de telles résonances ne peuvent être décrits en termes de superposition de fonctions propres de l’opérateur hamiltonien, c’est-à-dire d’invariants du mouvement. Les systèmes quantiques caractérisés par des temps de vie moyens, ou par des comportements correspondants à des « collisions », constituent donc la forme quantique des systèmes dynamiques au comportement chaotique (…)
L’abandon du modèle des systèmes intégrables a des conséquences aussi radicales en mécanique quantique qu’en mécanique classique. Dans ce dernier cas, il impliquait l’abandon de la notion de point et de loi d’évolution réversible qui lui correspond. Dans le second, il implique l’abandon de la fonction d’onde et de son évolution réversible dans l’espace de Hilbert. Dans les deux cas, cet abandon a la même signification : il nous permet de déchiffrer le message de l’entropie. (…)
La collision, transfert de quantité de mouvement et d’énergie cinétique entre deux particules, constitue, du point de vue dynamique, un exemple de résonance. Or, c’est l’existence des points de résonance qui, on le sait depuis Poincaré, empêche de définir la plupart des systèmes dynamiques comme intégrables. La théorie cinétique, qui correspond au cas d’un grand système dynamique ayant des points de résonance « presque partout » dans l’espace des phases , marque donc la transformation de la notion de résonance : celle-ci cesse d’être un obstacle à la description en termes de trajectoires déterministes et prédictibles, pour devenir un nouveau principe de description, intrinsèquement irréversible et probabiliste.
C’est cette notion de résonance que nous avons retrouvée au cœur de la mécanique quantique, puisque c’est elle qu’utilisa Dirac pour expliquer les événements qui ouvrent un accès expérimental à l’atome, l’émission et l’absorption de photons d’énergie spécifique, dont le spectre constitue la véritable signature de chaque type d’atome. (…) Le temps de vie, qui caractérise de manière intrinsèque un niveau excité, dépend, dans le formalisme actuel de la mécanique quantique, d’une approximation et perd son sens si le calcul est poussé plus loin. Dès lors, la mécanique quantique a dû reconnaître l’événement sans pouvoir lui donner de sens objectif. C’est pourquoi elle a pu paraître mettre en question la réalité même du monde observable qu’elle devait rendre intelligible. (…)
Pour expliquer les transitions électroniques spontanées qui confèrent à tout état excité un temps de vie fini, Dirac avait dû faire l’hypothèse d’un champ induit par l’atome et entrant en résonance avec lui. Le système fini que représente l’atome isolé n’est donc qu’une abstraction. L’atome en interaction avec son champ est, lui, un « grand système quantique », et c’est à son niveau que se produit la « catastrophe de Poincaré ».
L’atome en interaction avec le champ qu’il induit ne constitue pas, en effet, un système intégrable et ne peut donc pas plus être représenté par l’évolution de fonction d’onde qu’un système classique caractérisé par des points de résonance ne peut être caractérisé par une trajectoire. C’est là la faille que recélait l’édifice impressionnant de la mécanique quantique. (…) Il est significatif que, partout, nous ayons rencontré la notion de « brisement de symétrie ». Cette notion implique une référence apparemment indépassable à la symétrie affirmée par les lois fondamentales qui constituent l’héritage de la physique. Et, en effet, dans un premier temps, ce sont ces lois qui ont guidé notre recherche. (…) La description à symétrie temporelle brisée permet de comprendre la symétrie elle-même comme relative à la particularité des objets autrefois privilégiés par la physique, c’est-à-dire de situer leur particularité au sein d’une théorie plus générale. »

Poincaré invente le chaos déterministe

Le chaos dans le système solaire